Introduction to Markov Decision Processes
Markov Decision Processes (MDPs) form a mathematical framework that provides the foundation for many reinforcement learning algorithms. MDPs offer a way of modelling decision-making scenarios where outcomes are partly random and partly within the control of a decision-maker or agent.
Named after the Russian mathematician Andrey Markov, MDPs are a statistical model of a dynamic system whose behavior at each step depends only on its state at the previous step, not any earlier states, a concept known as the Markov property.
Elements of Markov Decision Processes
At their core, MDPs are defined by four key elements:
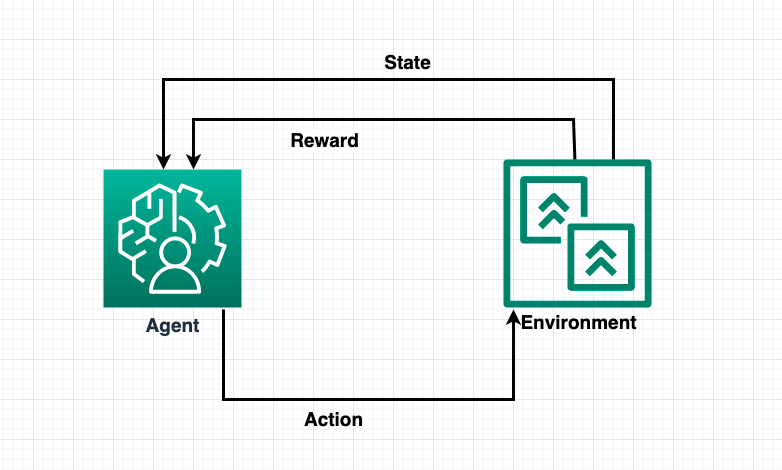
- States (S): States represent the different situations the agent could potentially be in. States can be anything from the position of a chess piece on a board, to the amount of money a gambler has left.
- Actions (A): Actions are the choices available to the agent in each state. Depending on the current state, the agent decides on the next action to take.
- Reward Function (R): Reward function determines the immediate reward received by the agent after performing an action in a given state. It is typically designed to encourage desirable behaviors.
- Transition Probability (P): Transition probability means that performing a certain action in a given state will lead to a certain subsequent state. It forms the ‘random’ part of the scenario and is often outside the agent’s control.
To these, we often add a policy (π), which is a rule the agent follows in deciding what actions to take based on the state it is in.
Examples of Markov Decision Process Problems
- Grid World: Grid World is a classic MDP problem where an agent must navigate a grid filled with rewards and obstacles. The states are the positions in the grid, actions are the movements (up, down, left, right), and rewards are given for reaching certain positions.
- Inventory Management: An MDP can model an inventory management problem. The states could be the current stock levels, actions could be the quantity to order, and rewards could be the profit from sales minus the cost of orders.
- Self-driving cars: The car, as an agent, needs to decide actions like accelerating, braking, or turning based on the current state, such as the position of other vehicles, traffic signals, and its own speed and direction.
In each of these scenarios, an optimal policy (π*) is the one that maximizes the total reward over time, guiding the agent towards the most beneficial actions given its state.
Markov Decision Processes in Game Theory
Game theory and MDPs intersect in multi-agent reinforcement learning, where multiple agents interact with the environment and with each other.
Each agent’s outcome depends not only on the environment but also on the actions of other agents. These situations can be modelled as Stochastic Games (or Markov Games), a generalization of MDPs to the multi-agent case.
In a Markov Game, each agent has its own reward function, and the state transition depends on the actions of all agents. Nash Equilibrium, a fundamental concept in game theory, is often used as a solution concept in these scenarios.
An equilibrium in this context is a set of policies, one for each agent, such that no agent can benefit from unilaterally deviating from its policy.
Conclusion:
Markov Decision Processes offer an effective framework for decision-making problems where outcomes are partly uncertain and partly under the control of a decision-maker.
MDPs lie at the heart of many reinforcement learning algorithms, helping to solve complex problems ranging from robotics to finance, supply chain management, and beyond.
